Case 1: Homogeneous
\begin{aligned}
ay'' + by' + cy &= 0\\\\
\text{Let } y &= e^{\lambda x}\\
y' &= \lambda e^{\lambda x}\\
y &= \lambda^2e^{\lambda x}
\end{aligned}\begin{aligned}
\text{Therefore, the auxiliary equation is }
a\lambda^2 + b\lambda + c = 0
\end{aligned}Case 1a
\begin{aligned}
b^2-4ac &> 0\;(\lambda = \lambda_1, \lambda = \lambda_2)\\
y &= C_1 e^{\lambda_1x} + C_2 e^{\lambda_2 x}
\end{aligned}Case 1b
\begin{aligned}
b^2-4ac &= 0\;(\lambda = \lambda_1)\\
y &= (C_1x + C_2) e^{\lambda_1x}
\end{aligned}Case 1c
\begin{aligned}
b^2-4ac &< 0\;(\lambda = p \pm iq)\\
y &= e^{px}(A\cos qx + B\sin qx)
\end{aligned}Case 2: Non Homogeneous
\begin{aligned}
ay'' + by' + cy &= d(x)\text{, where }d(x) \ne 0\\\\
y &= y_c + y_p\\\\
y_c &= \text{complementary function that satisfies }d(x) = 0\\
y_p &= \text{particular integral}\\
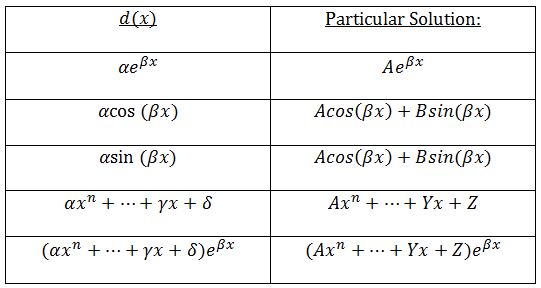
\end{aligned}To find yp, we make an educated guess using the method of undetermined coefficients. This works if d(x) is:
- Polynomial
- Exponential (i.e. Aekx, provided k is not a root of ay” + by’ + c = 0)
- Trigonometry (i.e. Asinkx + Bcoskx, provided ik is not a root of ay” + by’ + c = 0)
- Combination of polynomial, exponential, or trigonometry (provided d(x) does not contain part of yc)
Case 3: Euler Equation
\begin{aligned}
ax^2y'' + bxy' + cy &= g(x)\\\\
\text{Let }&y = x^\lambda\\
\text{Solve }&a\lambda^2 + (b-a)\lambda + c = 0\\
\end{aligned}Case 3a
\begin{aligned}
b^2 - 4ac &> 0\\
y &= Ax^{\lambda_1} + Bx^{\lambda_2}
\end{aligned}Case 3b
\begin{aligned}
b^2 - 4ac &= 0\\
y &= x^{\lambda}(A + B\ln x)
\end{aligned}Case 3c
\begin{aligned}
b^2 - 4ac &< 0\\
\lambda &= \alpha + i\beta\\
y &= x^{\alpha}(A\cos(\beta\ln x) + B\sin(\beta\ln x))
\end{aligned}
Leave a Reply