Model Selection

Alternatives to the Random Walk Model

Besides the random walk model, we have other types of models, including autoregressive, moving average, and ARMA models.

Autoregressive models have terms that depend on previous lagged returns (i.e. rt-k).

Moving average models have terms that depend on previous lagged innovations (i.e. previous random variables z_t-k).

ARMA models generate lagged correlations with AR and MA terms (i.e. ARMA = AR + MA).

RW, AR and ARMA models are expressed below.

RW

rt = μ + σzt

AR(1)

rt = c0 + c1rt-1 + σzt 

or

rt − μ = −λ(rt−1 − μ) + σ*zt, where μ = c0/(1+λ), λ = −c1

ARMA(p, q)

rt = c0 + c1rt-1 + …. + cprt-p + σzt + ɸ1zt-1 + … ɸqzt-q

How do we pick the correct model?

How do we pick the correct model? Is it AR1 or ARMA32? How do we pick the correct order of a model? Within each model, how do we determine its parameters?

To select the correct model, we want our estimator to obey a few rules. An estimator is a random variable that is a function of future observations (e.g. an estimate of the mean of future observations). 

Suppose θ-hat is an estimator and θ is the true value.

1. When we look at estimation, we want our estimators to be consistent. That is, in probability, they should converge to the true value.
2. We want them to be unbiased. In other words, the expectation of the estimator should be the true parameter value.
3. We want them to be asymptotically normal, so that we can apply our tests.

The three rules can be expressed mathematically as:

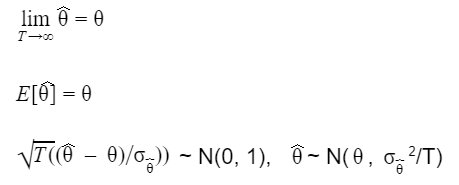
If we can find more than one model that satisfies the three rules above, we choose the most efficient model, possibly one with minimum variance, etc.

Example: AR Model

How do we do parameter estimation in AR(1)?

The AR(1) model is given by

rt − μ = −λ(rt−1 − μ) + σ*zt 

This can be rewritten as

rt = μ(1+λ) + (−λrt−1) + σ*zt

which expresses rt as a linear function yi = A + Bxi + εi

Therefore, we can use OLS (Ordinary Least Squares) to get values of the coefficients A and B.

How do we determine the order of a AR model?

To determine the order (i.e. is it AR1, AR2, or another order), we use the Partial Autocorrelation Function (PACF).

AR(n) is given by:

rt = c0(n) + c1(n)rt−1 +c2(n)rt−2 + … + cn(n)rt−n + σ(n)*zt

We select the order from the model with the largest number of non-negligible terms. In other words, if c4(4) onwards is negligible, we use order 3.