Import Libraries
# Import required libraries
import pandas as pd
import numpy as np
import warnings
warnings.filterwarnings('ignore')
# Get data
from sklearn.datasets import load_boston
from sklearn.metrics import mean_squared_error
Get Data
# Load data
boston_data = load_boston()
# Define feature and target
X = boston_data['data'] # Feature
y = boston_data['target'] # Label
# Subsume into a dataframe
boston = pd.DataFrame(boston_data['data'], columns=boston_data['feature_names'])
boston.head()
Explore Data
boston.shape
# Verify missing values on features
boston.isnull().sum()
# Verify missing values on labels
pd.DataFrame(y).isnull().sum()
boston.describe()
print(boston_data['DESCR'])
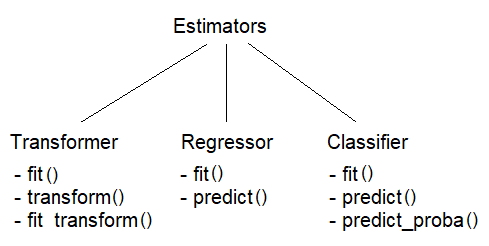
Overview of Scikit-Learn's API
Data Preprocessing
from sklearn.preprocessing import StandardScaler
# create and fit scaler
scaler = StandardScaler()
scaler.fit(X)
# scale data set
Xt = scaler.transform(X)
Model Training
Using Linear Regression¶
from sklearn.linear_model import LinearRegression, Lasso, Ridge
# Train Linear Regression model
model = LinearRegression()
model.fit(X, y) # training
# Predict label values on X
y_pred = model.predict(X) # predicting
print(y_pred[:10])
print(f'R2 Score: {model.score(X, y):0.4}')
How to improve R2 Score¶
- Remove outliers
- Test for multicollinearity and remove features
- Change the predictor
Using Gradient Boosting (Ensemble method)¶
from sklearn.ensemble import GradientBoostingRegressor
# create model and train/fit
model = GradientBoostingRegressor()
model.fit(X, y)
# predict label values on X
y_pred = model.predict(X)
print(y_pred[:10])
print(f'R2 Score: {model.score(X, y):0.4}')
Pipeline and FeatureUnion
Pipeline
- Predictor is always the last step in a pipeline
Pipelinearranges estimators in a series
FeatureUnion
FeatureUnionarranges transformers in parallel- It combines the output of the each of the transformers in parallel to generate one output matrix
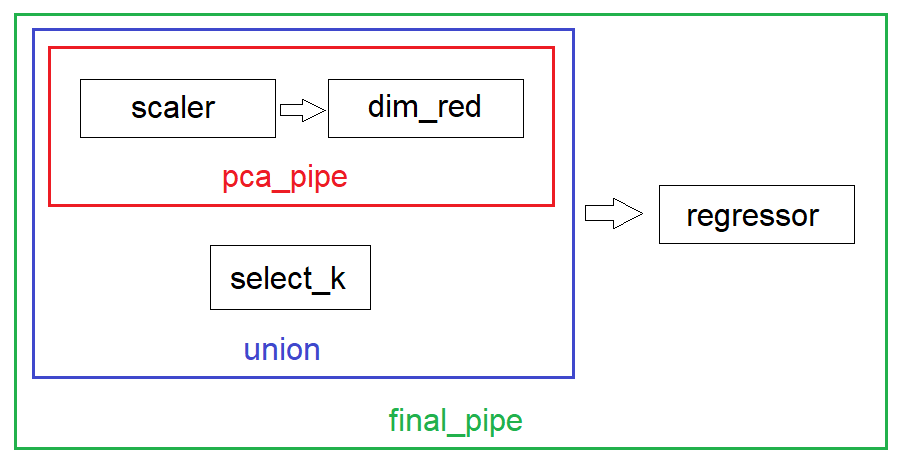
In the code below, pca_pipe gives us 4 features and selector gives us 2. Hence, we train our LinearRegression model using a total of 6 features.
from sklearn.pipeline import Pipeline, FeatureUnion
from sklearn.decomposition import PCA
from sklearn.feature_selection import f_regression, SelectKBest
# pca_pipe combines the scaling and dimensionality reduction steps
pca_pipe = Pipeline([('scaler', StandardScaler()), ('dim_red', PCA(n_components=4))])
# union combines pca_pipe with select_k in parallel to give us 6 features
union = FeatureUnion([('pca_pipe', pca_pipe), ('select_k', SelectKBest(f_regression, k=2))])
Training the model using a new pipeline final_pca¶
# final_pipe passes the 6 features to the predictor
final_pipe = Pipeline([('union', union), ('regressor', LinearRegression())]) # predictor is the last step
final_pipe.fit(X, y)
Overview of the Pipeline and FeatureUnion objects¶
Printing outputs of pca_pipe and union¶
pca_pipe.fit_transform(X)
As shown above, we end up with 4 features. For instance, for the first instance in the dataset, we end up with 4 features (i.e. dimensions) of values -2.09829747, 0.77311275, 0.34294273 and -0.89177403.
union.fit_transform(X, y)
Here, we end up with six features. The first 4 are from pca_pipe while the additional two are from select_k.
Custom Transformer
Scikit-learn has a base class called BaseEstimator that all estimators inherit.
Depending on the estimator type, they also inherit mixin classes such as RegressorMixin (for regressors), ClassifierMixin (for classifiers), and TransformerMixin (for transformers).
We can customize models by inheriting these classes and leverage on sklearn's functionalities such as Pipeline, GridSearchCV and such other features.
Description¶
In the code sample below, we create three variables X1, X2, and y, where y = X1 + 2*np.sqrt(X2).
If we try to use a linear regression model to fit these data, the model will not fit perfectly.
However, if we transform X2 to X2 = 2*np.sqrt(X2), we now have a perfect linear relationship, where y = X1 + X2. Training a linear regression model using X1, X2, and y will now give us a perfect fit (where RMSE = 0).
The code below demonstrates how to create a custom transformer to transform X2 to X2 = 2*np.sqrt(X2).
Code¶
# Creating X1, X2, and y and adding them to a DataFrame df
X1 = np.arange(1,21)
X2 = np.arange(11,31)
y = X1 + 2*np.sqrt(X2)
df = pd.DataFrame({'X1':X1, 'X2':X2, 'y': y}, columns = ['X1', 'X2', 'y'])
print(df.head())
# Split into training and test subsets (80:20)
train_X = df.iloc[:16, :-1]
test_X = df.iloc[16:, :-1]
train_y = df.iloc[:16, -1]
test_y = df.iloc[16:, -1]
# Training the model
lr1 = LinearRegression()
lr1.fit(train_X, train_y)
pred_y1 = lr1.predict(test_X)
print(f'{pred_y1}')
print(f'RMSE: {np.sqrt(mean_squared_error(test_y, pred_y1))}')
# Creating a custom transformer to transform X2 and train the linear regression model
from sklearn.base import BaseEstimator, TransformerMixin
# Build custom transformer SQRTTransformer that inherits BaseEstimator and TransformerMixin
class SQRTTransformer(BaseEstimator, TransformerMixin):
def __init__(self, feature):
self.feature = feature
def fit(self, X, y=None):
return self
def transform(self, X):
Xt = X.copy()
Xt[self.feature] = 2 * np.sqrt(Xt[self.feature])
return Xt
# Training the model again
pipe = Pipeline([('sqrt_trans', SQRTTransformer('X2')), # user defined
('regressor', LinearRegression())]) # from sklearn
pipe.fit(train_X, train_y)
pred_y2 = pipe.predict(test_X)
print(f'{pred_y2}')
print(f'RMSE: {np.sqrt(mean_squared_error(test_y, pred_y2)):.0f}')
Custom Regressor
In the code sample below, we build a custom regression that returns the mean of the y values passed to its fit() method.
from sklearn.base import RegressorMixin
# Build regressor
class MeanRegressor(BaseEstimator, RegressorMixin):
def __int__(self):
pass
def fit(self, X, y):
self.y_mean = np.mean(y)
return self
def predict(self, X):
return self.y_mean * np.ones(X.shape[0])
# Training a MeanRegressor model
mr = MeanRegressor()
mr.fit(train_X, train_y)
results = mr.predict(test_X)
results
Let's verify that 17.0330652 is indeed the mean of train_y
train_y.mean()
# Evaluating the performance of mr
print(f"R2 score: {mr.score(train_X, train_y)}") # score method inherited from base class
As expected, mr offers no improvement over using the mean as the predictor since all that it does is return the mean of the y values.