Import Libraries
In [1]:
# Data Manipulation
import numpy as np
import pandas as pd
import shap
# Visualizaiton
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
# Get Dataset from Scikit-learn
from sklearn.datasets import load_boston
# Data Preprocessing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
# Regressor
from sklearn.linear_model import LinearRegression, Lasso, Ridge, ElasticNet
# Metrics
from sklearn.metrics import mean_squared_error, r2_score
Load Data into DataFrame
In [2]:
# Load data
boston_data = load_boston()
# Subsume into a dataframe
boston = pd.DataFrame(boston_data['data'], columns=boston_data['feature_names'])
# Add target to the dataframe
boston['MEDV'] = boston_data.target
boston
Out[2]:
Split Data into Training and Test Subsets
In [3]:
# Splitting the datasets into training and testing data.
X_train, X_test, y_train, y_test = train_test_split(boston.iloc[:, :-1], boston.iloc[:, -1], test_size=0.2, random_state=0)
# Output the train and test data size
print(f"Train and Test Size {len(X_train)}, {len(X_test)}")
Linear Regression
In [4]:
pipe = Pipeline([
('scaler', StandardScaler()),
('regressor', LinearRegression())
])
In [5]:
# fit/train model
pipe.fit(X_train, y_train)
# predict labels
y_pred = pipe.predict(X_test)
# metrics
rmse = mean_squared_error(y_test, y_pred, squared=False)
print(f'RMSE: {rmse:0.4}')
print(f'R^2 Train: {pipe.score(X_train, y_train):0.4}')
print(f'R^2 Test: {pipe.score(X_test, y_test):0.4}')
In [6]:
pipe['regressor'].coef_
Out[6]:
In [7]:
pipe['regressor'].intercept_
Out[7]:
LASSO Regression
The Least Absolute Shrinkage and Selection Operator (LASSO) is a variation of linear regression where a L1 penalty term is added to the Mean Square Error (MSE).
This penalty term is calculated by summing the absolute values of the regression weights (i.e. the coefficients), multiplied by a constant known as the regularization penalty, denoted as lamda in the formula below (but as alpha in sklearn).
The L1 penalty term not only shrinks the regression weights, but also shrinks some of them to zero, making it very useful for feature selection.
The loss function for LASSO regression is given by:
In [8]:
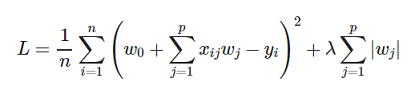
lasso = Pipeline([
('scaler', StandardScaler()),
('regressor', Lasso(alpha=0.1))
])
In [9]:
# fit lasso model
lasso.fit(X_train, y_train)
print(f'R^2 Train: {lasso.score(X_train, y_train):0.4}')
print(f'R^2 Test: {lasso.score(X_test, y_test):0.4}')
In [10]:
lasso['regressor'].coef_
Out[10]:
Effects of Lambda on Model¶
In [11]:
alpha_range = np.linspace(0.01,10,100)
la_coef = []
la_score = []
la_rmse = []
for i in alpha_range:
lasso = Pipeline([('scaler', StandardScaler()), ('regressor', Lasso(alpha=i))])
lasso.fit(X_train, y_train)
y_pred = lasso.predict(X_test)
la_coef.append(lasso['regressor'].coef_)
la_rmse.append(mean_squared_error(y_test, y_pred, squared = False))
la_score.append(r2_score(y_test, y_pred))
Coefficients as a function of Lambda¶
In [12]:
# Plot Coefficients
fig = plt.figure(figsize=(20,8))
ax = plt.axes()
ax.plot(alpha_range, la_coef)
ax.set_xscale('log')
ax.set_xlim(ax.get_xlim()[::-1]) # reverse axis
ax.set_title('Lasso coefficients as a function of lambda')
ax.set_xlabel('$\lambda$ in descending order')
ax.set_ylabel('$\mathbf{w}$');
Each line above represents a coefficient of the LASSO regression model.
We see that when lambda is huge (10), all coefficients become zero. When lambda is 1, most coefficients (all except 3) are close to zero.
RMSE and R2 as a function of lambda¶
In [13]:
# Plot RMSE
fig, ax = plt.subplots(1,2, figsize=(20,8))
ax[0].plot(alpha_range, la_rmse, 'orange')
ax[0].set_title('Root Mean Square Error')
ax[0].set_xlabel('Alpha')
ax[0].set_ylabel('RMSE')
# Plot R^2
ax[1].plot(alpha_range, la_score, 'r-')
ax[1].set_title('Coefficient of Determination')
ax[1].set_xlabel('Alpha')
ax[1].set_ylabel('R-Squared');
Ridge Regression
In ridge regression, the cost function is altered by adding a L2 penality equivalent to square of the magnitude of the coefficients. The Ridge regression shrinks the coefficients and helps to reduce the multi-collinearity.
Its cost function is given by:
In [14]:
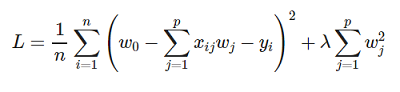
rid = Pipeline([
('scaler', StandardScaler()),
('regressor', Ridge(alpha=1))
])
In [15]:
# fit ridge model
rid.fit(X_train, y_train)
print(f'R^2 Train: {rid.score(X_train, y_train):0.4}')
print(f'R^2 Test: {rid.score(X_test, y_test):0.4}')
In [16]:
rid['regressor'].coef_
Out[16]:
Effects of Lambda on Model¶
In [17]:
alpha_range = 10**np.linspace(6,-2,100)*0.5
rid_score = []
rid_rmse = []
rid_coef = []
for i in alpha_range:
rid = Pipeline([('scaler', StandardScaler()), ('regressor', Ridge(alpha=i))])
rid.fit(X_train, y_train)
y_pred = rid.predict(X_test)
rid_coef.append(rid['regressor'].coef_)
rid_rmse.append(mean_squared_error(y_test, y_pred, squared = False))
rid_score.append(r2_score(y_test, y_pred))
Coefficients as a function of Lambda¶
In [18]:
# Plot Coefficients
fig = plt.figure(figsize=(20,8))
ax = plt.axes()
ax.plot(alpha_range, rid_coef)
ax.set_xscale('log')
ax.set_xlim(ax.get_xlim()[::-1]) # reverse axis
ax.set_title('Ridge coefficients as a function of lambda')
ax.set_xlabel('$\lambda$ in descending order')
ax.set_ylabel('$\mathbf{w}$');
RMSE and R2 as a function of lambda¶
In [19]:
# Plot RMSE
fig, ax = plt.subplots(1,2, figsize=(20,8))
ax[0].plot(alpha_range, rid_rmse, 'orange')
ax[0].set_title('Root Mean Square Error')
ax[0].set_xlabel('$\lambda$')
ax[0].set_ylabel('RMSE')
ax[0].set_xscale('log')
# Plot R^2
ax[1].plot(alpha_range, rid_score, 'r-')
ax[1].set_title('Coefficient of Determination')
ax[1].set_xlabel('$\lambda$')
ax[1].set_ylabel('$R^2$')
ax[1].set_xscale('log');
ElasticNet Regression
ElasticNet combines the properties of both Lasso and Ridge regression. It penalizes the model using both the L1 and L2 norm.
In the formula below, Elastic Net is the same as LASSO when alpha = 1 and ridge when alpha = 0. For other values of alpha, the penalty term interpolates between the L1 and L2 penalty terms.
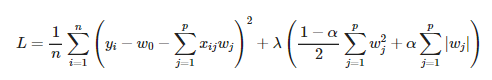
Note: lambda = alpha and alpha = l1_ratio in sklearn.
In [20]:
elastic = Pipeline([
('scaler', StandardScaler()),
('regressor', ElasticNet(alpha=0.1, l1_ratio=0.5))
])
In [21]:
# fit elasticnet model
elastic.fit(X_train, y_train)
print(f'R^2 Train: {elastic.score(X_train, y_train):0.4}')
print(f'R^2 Test: {elastic.score(X_test, y_test):0.4}')
In [22]:
elastic['regressor'].coef_
Out[22]:
Effects of Lambda on Model¶
In [23]:
alpha_range = 10**np.linspace(2,-2,100)*0.5
elastic_score = []
elastic_rmse = []
elastic_coef = []
for i in alpha_range:
elastic = Pipeline([('scaler', StandardScaler()), ('regressor', ElasticNet(alpha=i))])
elastic.fit(X_train, y_train)
y_pred = elastic.predict(X_test)
elastic_rmse.append(mean_squared_error(y_test, y_pred, squared = False))
elastic_coef.append(elastic['regressor'].coef_)
elastic_score.append(r2_score(y_test, y_pred))
Coefficients as a function of Lambda¶
In [24]:
# Plot Coefficients
fig = plt.figure(figsize=(20,8))
ax = plt.axes()
ax.plot(alpha_range, elastic_coef)
ax.set_xscale('log')
ax.set_xlim(ax.get_xlim()[::-1]) # reverse axis
ax.set_title('ElasticNet coefficients as a function of the regularization')
ax.set_xlabel('$\lambda$ in descending order')
ax.set_ylabel('$\mathbf{w}$');
RMSE and R2 as a function of lambda¶
In [25]:
# Plot RMSE
fig, ax = plt.subplots(1,2, figsize=(20,8))
ax[0].plot(alpha_range, elastic_rmse, 'orange')
ax[0].set_title('Root Mean Square Error')
ax[0].set_xlabel('Alpha')
ax[0].set_ylabel('RMSE')
# Plot R^2
ax[1].plot(alpha_range, elastic_score, 'r-')
ax[1].set_title('Coefficient of Determination')
ax[1].set_xlabel('Alpha')
ax[1].set_ylabel('R-Squared');
