This tutorial shows an example of using Q learning to find the best path. Consider the following scenario, where our objective is to get out of the walled interior (i.e. to move to region 5). Any action that results in us being in region 5 gives us a reward of 100; all other actions give us a reward of 0.

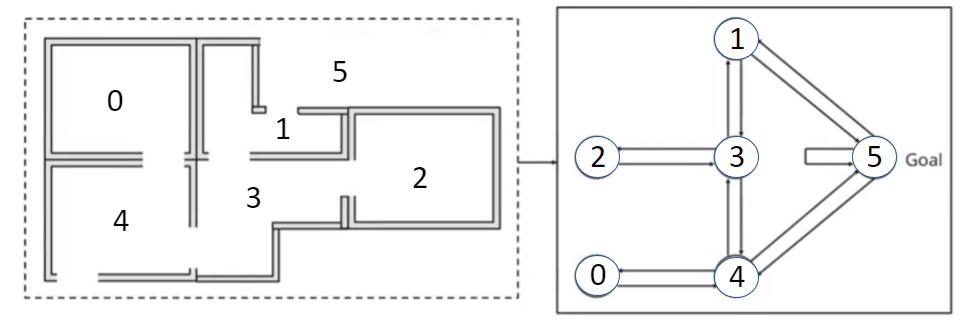
Suppose we are in region 1 and move to region 5, we denote this scenario as the (state, action) pair (1, 5).

To calculatet the Q value for this (state, action) pair, we use the bellman equation:

$Q(S_t,A_t) = R_t + \gamma \underset{a}{\max} Q(S_{t+1},a)$

where,
$S_t$ is the state at timestep $t$,
$A_t$ is the action taken at state $S_t$,
$R_{t+1}$ is the direct reward of action $A_t$,
$ \gamma $ is the discount factor ranging $0 \leq \gamma \leq 1$, and
$\underset{a}{\max} Q(S_{t+1},a)$ is the maximum delayed reward given the optimal action from the current policy Q.

Suppose we set $ \gamma $ as 0.8. At the start, all the Q values are 0.

As mentioned above, suppose we start from region 1 and move to region 5. After moving to region 5, we can remain in region 5, move to region 4, or move to region 1. Therefore, there are three possible $ Q(S_{t+1},a) $ pairs, namely: (5, 5), (5, 4), or (5, 1).

As the initial Q values are all 0, $\underset{a}{\max} Q(S_{t+1},a)$ is 0.

With these values, we can now update the Q value for (1, 5).

Q(1, 5) = 100 + 0.8*(0) = 100

To find the optimal policy, we use iteration to update the Q values. $Q_i$ will eventually converge to the optimal $Q^*$ as $i\to\infty$.

Python Implementation

The Python implementation is given below:

In [1]:
# import libraries
import numpy as np
import warnings
warnings.filterwarnings('ignore')
In [2]:
# create the reward matrix
R = np.array([[-1,-1,-1,-1,0,-1],
             [-1,-1,-1,0,-1,100],
             [-1,-1,-1,0,-1,-1],
             [-1,0,0,-1,0,-1],
             [0,-1,-1,0,-1,100],
             [-1,0,-1,-1,0,100]])

R[1, 5] means state = 1 and action = 5. In other words, we are in region 1 and move to region 5. This gives us a reward of 100.

In [3]:
R[1, 5]
Out[3]:
100

A reward of -1 means that (state, action) pair is invalid. For instance, we cannot move from region 4 to 2. Hence, (4, 2) is invalid.

In [4]:
R[4, 2]
Out[4]:
-1
In [5]:
# Initialize the Q matrix with zeroes
Q = np.array(np.zeros([6,6]))
print(f'Q Matrix \n \n {Q}')

Q Matrix 
 
 [[0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0.]]
In [6]:
# Initial State - choosen at random
initial_state = 1

# Gamma (discount paramaters)
gamma = 0.8
In [7]:
# Function that returns all available actions for a specified state
def available_actions(state):
    current_state_row = R[state]
    aaction = np.where(current_state_row >=0)[0]
    return aaction
In [8]:
# Get available actions in the current state (1)
available_act = available_actions(initial_state)
available_act
Out[8]:
array([3, 5], dtype=int64)
In [9]:
# Function that returns the next action to be performed
def next_action(available_action_range):
    naction = int(np.random.choice(available_act,1))
    return naction
In [10]:
# Get next action (In our example, we randomly choose between action 3 and 5)
action = next_action(available_act)
action
Out[10]:
5
In [11]:
# Function to update the Q Matrix
def update(current_state, action, gamma):
    max_index = np.where(Q[action,] == np.max(Q[action,]))[0]
    
    if max_index.shape[0] > 1: # if there is more than one (state, action) with the highest Q value, choose one randomly
        max_index = int(np.random.choice(max_index,size=1))
    else:
        max_index = int(max_index)
    
    max_value = Q[action, max_index]
    
    # Q learning formula
    Q[current_state, action] = R[current_state, action] + gamma * max_value
In [12]:
# Update Q-matrix for the (1, 5) pair
update(initial_state, action, gamma)
In [13]:
# Q(1, 5) = 100 + 0.8(0) = 100
Q[1, 5]
Out[13]:
100.0

Training

In [14]:
# Training for 10000 iterations

for i in range(10000):
    current_state = np.random.randint(0,int(Q.shape[0]))
    available_act = available_actions(current_state)
    action = next_action(available_act)
    update(current_state, action, gamma)
In [15]:
# Normalize the Q matrix
print(f'Trained Q-Matrix \n \n {Q/np.max(Q)*100}')

Trained Q-Matrix 
 
 [[  0.    0.    0.    0.   80.    0. ]
 [  0.    0.    0.   64.    0.  100. ]
 [  0.    0.    0.   64.    0.    0. ]
 [  0.   80.   51.2   0.   80.    0. ]
 [ 64.    0.    0.   64.    0.  100. ]
 [  0.   80.    0.    0.   80.  100. ]]

Testing

In [16]:
current_state = 2
steps = [current_state]

while current_state !=5:
    next_step_index = np.where(Q[current_state,] == np.max(Q[current_state,]))[0]
    
    if next_step_index.shape[0] > 1:
        next_step_index = int(np.random.choice(next_step_index,size=1))
    else:
        next_step_index = int(next_step_index)
        
    steps.append(next_step_index)
    current_state = next_step_index
In [17]:
# Print selected sequence of steps
print(f'Selected Path {steps}')

Selected Path [2, 3, 1, 5]